일반적으로 신경망이 깊어질수록 입력 데이터에 대한 보다 높은 수준의 특징을 학습할 수 있을 것이라 알려져있습니다. 하지만 실제 연구 결과 신경망이 깊어져도 training error가 줄어들지 않는 degradation 문제가 발생했습니다. Resnet은 이에 대한 해답을 훌륭하게 제시합니다. Resnet은 image classificatioin 분야는 물론 image detection 분야에도 영향을 끼치는 중요한 모델입니다. 이에 대해 심도 있게 살펴보고자 관련 논문 2편을 살펴보고 정리해보았습니다.

깊은 신경망의 문제점

• Deep Residual Learning for Image Recognition 논문에서는 신경망이 깊어짐에 따라 발생하는 degradation 문제는 단순히 vanishing gradients이나 overfitting에 기인한 것이 아니라고 합니다. 모델에 Batch normalization을 추가하여 적절한 정규화를 통해 신경망의 신호가 잘 전달되도록 유도하여 vanishing gradients 문제를 어느 정도 해결했으며, validation error와 training error의 차이로 확인할 수 있는 overfitting 문제는 더더욱 아니기 때문입니다.

위의 그래프는 20층의 신경망과 56층의 신경망의 학습 및 테스트 error 결과를 반영한 도표입니다. 보시다시피 층이 깊어졌음에도 불구하고 error가 하락하지 않는 문제가 발생했습니다.

Resnet 연구팀은 degradation의 원인으로 신경망이 깊어짐에 따라 최적화(optimization)가 제대로 이뤄지지 않음을 지적합니다. 최적화가 제대로 수행되기 어려운 이유는

• 신경망이 깊어짐에 따라 학습해야할 파라미터 수가 매우 많아지기 때문에

• 신경망은 수많은 non-linaer 함수의 연속으로 이뤄지기 때문에 최적화하고자 하는 objective function이 non-convex 형태가 되기 때문에(non-convex function은 convex function보다 최적화하기 힘듭니다;)

위와 같은 문제를 해결하기 위해 연구팀은 identity mapping을 활용합니다.

Identity mappings

• 신경망은 입력값에 대한 최적의 출력값을 산출하는 함수(mapping)를 학습합니다. 신경망이 학습한다는 것은 최적의 mapping을 학습하는 것이라고 할 수 있습니다. Identity mapping이란 입력값과 동일한 출력값을 산출하는 mapping입니다. 즉 입력값을 x, mapping을 h, 출력값을 h(x)라고 했을 때 x = h(x)인 경우를 의미합니다.

• Resnet 연구팀은 한 가지 가정을 합니다. 층이 깊어질수록 최적화하기가 힘들다면 얕은 층에 identity mapping을 학습하는 layer만을 추가하여 최적화하기 더 쉽게 만들어주면 어떨까? 예를 들어 20층 신경망에 identity mapping을 수행하는 신경망 층을 추가한다면 앞선 20층에서 출력한 값을 그대로 신경망 끝까지 전달할 수 있을 것입니다. 즉 연구팀은 이러한 방식을 통해 training error가 20층 신경망에 비해 더 늘어나지 않고, 다시 말해 degradation 문제가 발생하지 않으며, 동시에 신경망이 깊어짐에 따라 더 고수준의 특징을 학습하는 장점을 얻을 수 있을 것이라 가정한 것입니다.

• 하지만 앞서 살펴보았듯이 깊은 신경망은 non-linear function의 연속으로 identity mapping조차 학습시키기 어렵다는 문제가 있습니다. 이에 대한 해답으로 연구팀은 residual block을 추가하는방식을 제시합니다.

Residual block

• Residual block은 최적화해야할 mapping을 기존 mapping인 h와 입력값x의 차이인 F(x)(=h(x)-x)로 변환한 연속된 layer를 의미합니다. 기존 방식으로 identity mapping을 할 경우 h(x)를 알 수 없는 값으로 직접 최적화해야하는 어려움이 있습니다. 하지만 Residual block에서는 F(x)가 0이 되도록 학습하면 h(x)=x가 되어, Identity mapping을 수행하는 것이 상대적으로 용이합니다.

• 논문에서는 F(x)=0 이 되도록 최적화한다는 조건(Pre-conditioning)이 추가되어 identity mapping을 학습이 쉬워진다고 합니다. 또한 기존의 mapping을 input data를 참조하지 않는 unreferenced mapping으로, residual block을 input data를 참조하는 referenced mapping이라고 언급합니다.

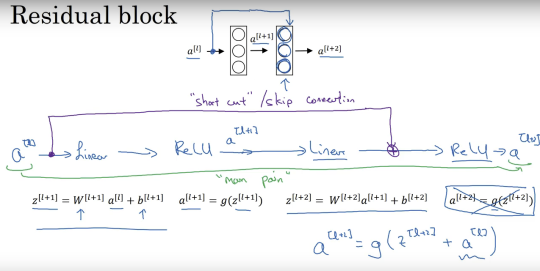
• Resicual block은 위와 같이 input data를 출력단에 non-linear 함수(여기서는 ReLU)를 적용하기 전에 더해주는 방식을 통해 구현할 수 있습니다. 이와 같은 방식을 skip connection이라고 합니다.

• Residual block에서 Identity mapping에 대한 학습이 효과적인 이유는 후속 논문인 Identity Mappings in Deep Residual Networks에서 자세히 설명합니다. 이에 대해 간략히 살펴보도록 하겠습니다.(latex 수식이 깨져보일 경우 새로고침을 하면 잘 보입니다) \[x_l : 입력값 \\ W_l : 가중치 행렬 \\ F(x_l, W_l) : residual\ mapping \\ f : activation \ function(=ReLU) \\ y : 출력값 \\ x_{l+1} : 다음 층의 입력값 \\ \mathcal E : loss \ function\]

  이라고 했을 때 layer의 출력값은 다음과 같습니다. \[y_l = h(x_l) + F(x_l, W_l) \\ x_{l+1} = f(y_l)\]

  이 때, 계산의 편의를 위해 활성화 함수 \(f\)를 identity mapping이라고 하면 \(x_{l+1} = y_l\) 이 성립합니다. 따라서 아래의 식도 성립합니다. \[x_{l+1} = x_l + F(x_l, W_l) \\ x_{l+2} = x_l + F(x_l, W_l) + F(x_{l+1}, W_{l+1}) \\ x_L = x_l + \sum_{i=l}^{L-1}F(x_i, W_i)\]

  즉 순전파 시 Residual block을 통해 신경망을 residual mapping의 합으로 표현할 수 있습니다. 또한 역전파 진행 시 수식을 살펴보면 다음과 같습니다. \[\frac{\partial \mathcal E}{\partial x_L} = \frac{\partial \mathcal E}{\partial x_L}\frac{\partial x_L}{\partial x_l} = \frac{\partial \mathcal E}{\partial x_L}(1 + \frac{\partial}{\partial x_l}\sum_{i=l}^{L-1}F(x_i, W_i))\]

  위와 같은 경우 다음과 같은 두 항으로 분리하여 생각해볼 수 있습니다.

  1) \(\frac{\partial \mathcal E}{\partial x_L}\) : loss function에 대한 마지막 신경망의 출력값의 미분값이므로 어떠한 신경망도 거치지 않고 모든 층에 동일한 값을 전달할 수 있습니다.

  2) \((1 + \frac{\partial}{\partial x_l}\sum_{i=l}^{L-1}F(x_i, W_i))\) : 각 층의 residual mapping에 대한 미분값으로 뒤의 항이 -1이 되어 전체가 0이 되는 경우는 극히 드물기 때문에 gradient vanishing 문제가 발생하지 않습니다.

     즉 residual block을 통해 identity mapping을 학습시킬 경우 forward propagate, backpropagate 모두 덧셈을 통해 신호가 전달되기 때문에 최적화시키기 용이하며 vanishing gradients 문제도 발생하지 않습니다.

Conclusion

• 지금까지 Resnet의 원리에 대해 살펴보았습니다. Resnet은 residual block 구조를 통해 신경망이 identity mapping을 학습하기 용이한 환경을 제공하였습니다. 이를 통해 최적화가 보다 잘 이뤄지고 신경망의 신호가 효과적으로 전달되어 신경망이 깊어져 발생하는 degradation 문제를 해결하였습니다.

• 수많은 블로그를 통해 Resnet을 이해하려 했지만 역시 논문만큼 잘 설명한 곳은 없더군요… 아직 Resnet을 완벽하게 이해한 것도 아니고 전체 Resnet 구조에 대해서도 좀 더 살펴보고 싶기 때문에 논문을 다시 읽어볼 예정입니다!

Reference

Deep Residual Learning for Image Recognition
Identity Mappings in Deep Residual Networks
Why are deep neural networks are hard to train?
Andrew Ng(youtube) - Resnet
Andrew Ng(youtube) - Why Resnets work?