최근까지 CNN 연구는 주로 이미지 인식의 정확도를 높히는 방법에 집중하였습니다. 하지만 이러한 연구 결과를 실생활에서 적용하기 위해서는 모델의 성능만큼이나 모델의 크기 역시 중요합니다. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size 논문에서는 SqueezeNet 모델을 통한 모델 경량화와 그 이점에 대해 설명합니다.

모델 경량화의 이점

1) More efficient distributed training 병렬 학습 시 서버와의 소통으로 발생하는 과부하는 파라미터의 수에 비례합니다. 더 적은 파라미터는 더 빠른 학습을 가능케합니다.

2) Less overhead when exporting new models to clients 자율주행차같은 경우 새로운 모델을 서버를 통해 고객의 차로 전송합니다(이러한 방식을 over-the-air update라고 합니다). 작은 모델은 서버와의 소통이 적어 더 잦은 업데이트가 가능할 것입니다.

3) Feasible FPGA and embedded deployment FPGA(field programmable gate array, 프로그래밍 가능한 반도체라고 합니다)에 직접 모델을 직접 저장할 수 있어 병목 현상이 상대적으로 적습니다.

SqueezeNet의 전략

SqueezeNet은 모델 경량화를 통해 AlexNet보다 50배 이상 적은 파라미터를 가지지만 비슷한 수준의 정확도를 보입니다. 또한 감소된 파라미터 수로 인해 0.5MB 이하의 용량을 차지합니다. 논문에서는 이러한 SqueezeNet 구현을 위해 3가지 전략을 제시합니다.

1) Replace 3x3 filters with 1x1 filters 1x1 filter를 사용할 경우 3x3 filter를 사용할 때보다 파라미터 수가 9배나 적습니다. 따라서 layer마다 3x3 filter를 사용하는 횟수를 줄임으로서 파라미터 수를 감소시킬 수 있습니다.

2) Decrease the number of input channels to 3x3 filters 1)에서 언급했던 것과 같이 3x3 filter의 수를 줄일 뿐만 아니라 3x3 filter가 적용되는 input channel의 수를 줄이면 파라미터의 수를 줄이는 데 효과적입니다.

3) Downsample late in the network so that convolution layers have large activation

• 일반적으로 pooling을 적용하거나 stride를 높히는 방식을 통해 이미지의 spatial resolution(저는 이미지의 높이, 넓이로 이해했습니다)을 줄이는 downsample을 시행합니다. 논문의 저자들은 모든 조건이 동일할 때 더 큰 activation map이 더 높은 정확도를 가진다고 가정합니다. 따라서 downsample 과정을 네트워크 후반부로 미룬다면 더 큰 activation map을 보존하는 것이 가능해지고 이는 곧 모델의 성능과도 직결됩니다.

• 전략 1), 2)가 파라미터 수를 줄이는 방안이라면 전략 3)은 정확도를 보존하는 전략이라고 할 수 있습니다. 전략 3)은 제한된 파라미터 수에서 정확도를 최대화시키는 방법입니다. 지금까지 살펴본 SqueezeNet의 전략은 Fire module을 통해 구현할 수 있습니다.

Fire Module

Fire Module은 squeeze layer와 expand layer로 구성됩니다. 먼저 squeeze layer에서 1x1 filter를 적용하고, expand layer에서 1x1 filter와 3x3 filter를 순차적으로 적용합니다.

• 1x1 filter를 사용함으로써 파라미터 수를 줄임으로서 앞서 언급했던 전략 1)을 수행하였습니다.

• Fire Module에서 \(s_{1x1}\)은 squeeze layer의 1x1 filter의 수, \(e_{1x1}, e_{3x3}\),은 각각 expand layer의 1x1 filter, 3x3 filter의 수입니다. Fire Module에서는 하이퍼파라미터를 \(s_{1x1} < (e_{1x1} + e_{3x3})\) (squeeze layer의 filter 수를 expand layer의 filter 수보다 작게 함으로써)으로 구성함으로써 3x3 filter가 적용되는 input channel의 수를 줄였습니다. 이를 통해 전략 2)를 효과적으로 구현했습니다.

다음은 Fire Module를 상세하게 표현한 그림입니다. Squeeze layer와 expand layer가 순차적으로 적용되는 것을 확인할 수 있습니다.

저는 이 부분에서 의문이 들었습니다. 파라미터 수를 효과적으로 줄이기 위해서라면 3x3 filter를 적용할 필요가 있을까? 전부 다 1x1 filter를 적용하면 되지 않을까? 하지만 1x1 filter만을 적용할 경우 filter가 적용되는 주변 값에 대한 정보를 얻을 수 없어 신경망의 표현력이 제한된다고 합니다. 즉 신경망의 정확도가 낮아질 수 있다는 것입니다.

3x3 filter에 대해 검색하면서 짝수 크기의 filter, 가령 2x2 크기의 filter는 사용하지 않는다는 이유도 알게 되었습니다. 짝수 크기의 filter의 경우 filter가 적용되는 map의 중앙에 대한 정보를 효과적으로 추출하지 못한다고 합니다.

SqueezeNet Architecture

SqueezeNet은 conv layer를 시작으로 8개의 Fire Module을 거쳐 conv layer로 마무리됩니다. 논문 저자들은 filter의 수를 점차 증가시켰고 pooling layer를 conv1, fire4, fire8, conv10에 적용한다고 합니다. 이는 downsample을 상대적으로 늦게 적용하는 전략 3)에 따른 것입니다.

• 1x1 filter와 3x3 filter가 같은 높이와 넓이를 가지게 하기 위해 1-pixel 크기의 zero-padding을 추가했습니다.

• 활성화 함수로 ReLU를 사용했습니다.

• Dropout 비율을 50%로 적용했습니다.

• NiN(Network in Network) 논문을 참고하여 마지막에 fully-connected layer가 아니라 Global average pooling을 적용했습니다. 신경망 마지막단에 fully-connected layer를 적용할 경우 overfitting이 발생할 가능성이 크다고 합니다. Global average pooling을 적용할 경우 학습해야할 파라미터가 없고, overfitting에 보다 강건하다고 합니다.

• 처음 학습을 시작할 때 learning rate를 0.04로 지정하고 점차 감소시켰습니다.

Evaluation

아래는 AlexNet의 파라미터 수를 도표로 나타낸 결과입니다. 보시다시피 총 600만개가 넘는 파라미터를 학습시켜야 합니다.

다음으로 SqueezeNet의 파라미터 수를 세부적으로 나타낸 도표입니다. 총 120만개 이상의 학습 가능한 파라미터가 있습니다.

SqueezeNet을 사용한 결과 AlexNet보다 파라미터 수를 50배 이상 감소시켰으며 정확도 측면에서 근접하거나 초과하는 성능을 보였습니다.

세부적인 탐색

논문의 저자들은 여기서 그치지 않고 모델의 성능을 개선할 수 있는 부분을 모델의 layer 측면을 살펴보는 microarchitecture 부분과, 모델의 전체 구조인 macroarchitecture로 나눠 세부적으로 살펴봅니다.

Microarchitecture

Fire Module의 하이퍼파라미터는 3개이며 SqueezeNet은 총 8개의 Fire Module로 구성되어 있으므로 총 24개의 하이퍼파라미터를 가집니다. 논문 저자는 24개의 하이퍼파라미터를 통제하는 파라미터를 메타파라미터(metaparameter)라고 부릅니다. Microarchitecture 부분에서는 메타파라미터를 조정하면서 모델의 크기와 성능에 미치는 영향을 분석합니다.

\(base_e\) : 첫 Fire Module의 expand filter의 수
\(freq\) : Fire Module의 수
\(i\) : Fire Module의 차수(~번째 Fire Module)
\(incre_e\) : 증가시킬 expand filter의 갯수
\(e_i\) : expand filter의 수
\(pct_{3x3}\) : expand filter에서 3x3 filter의 비율
\(SR\) : squeeze layer filter의 전체 비율(Squeeze Ratio)

메타 파라미터가 위와 같을 때 아래와 같은 등식이 성립합니다. \[e_i = base_e + (incre_e * (i / freq))\\e_i = e_{i,1x1} + e_{i,3x3}\\ e_{i,3x3} = e * pct_{3x3}\\s_{1x1} = SR * e_i\\\]

SqueezeNet에서 메타 파라미터는 다음과 같이 지정했습니다. \[base_e = 128, incre_e= 128, freq = 2, SR =0.125\]

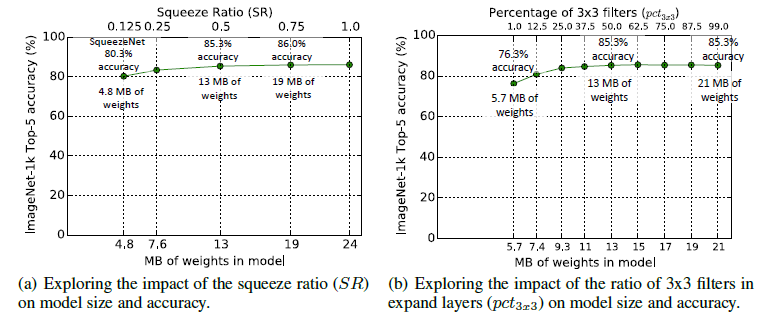
• 왼쪽 도표는 SR이 모델의 크기와 성능에 미치는 영향을 분석한 결과입니다. 실험 결과 SR이 0.125보다 높게 설정할 경우 모델의 크기가 커지지만 정확도가 올라갑니다. SR을 0.75로 지정한 경우 19MB의 크기를 가지면서 86%의 정확도를 보입니다. 추가적으로 SR을 증가시켰지만 모델의 크기만 커질 뿐 정확도는 향상되지 않았습니다.

• 오른쪽 도표는 expand layer에서 1x1과 3x3 filter의 비율이 모델 사이즈와 정확도에 주는 영향에 대해 실험한 결과를 보여줍니다. 실험 결과 pct가 50%일 때, 즉 3x3 filter와 1x1 filter의 수가 같을 때 가장 높은 정확도를 보였고, 이후 pct를 증가시켜도 성능은 향상되지 않았습니다.

Macroarchitecture

다음으로 논문에서는 Macroarchitecture 부분을 살펴보기 위해 모델 전체 구조를 변형시켜 비교함으로써 모델의 크기와 정확도에 미치는 영향을 탐색하였습니다.

• 논문 저자들은 ResNet에서 사용된 skip connection을 활용하여 bypass connection이 적용된 모델 구조를 만들었습니다. 더 나아가 input과 output이 같은 수의 channel을 가지게 하기 위해 1x1 convolution을 추가한 Complex bypass connection이 적용된 모델도 만들었습니다. 논문에서는 일반 SqueezeNet인 Vaniila SqueezeNet의 성능을 bypass connection이 적용된 모델과 complex bypass connection이 적용된 모델과 비교합니다.

• 실험 결과 모델 구조를 변경한 두 경우 모두 일반적인 Vanilla SqueezeNet보다 높은 정확도를 보였습니다. 하지만 Bypass connection을 적용한 모델이 Complex bypass connection을 적용한 모델보다 더 높은 정확도를 보였습니다(물론 모델 크기도 더 작습니다).

Conclusion

SqueezeNet은 모델의 정확도를 유지하면서 모델의 크기를 효과적으로 줄였습니다. 이러한 강점으로 임베디드 현장에서 큰 호평을 받았다고 합니다. Rawberry Pi에서도 돌아간다고 하니 다음에는 SqueezeNet을 탑재한 임베디드 프로젝트를 진행해보고 싶다는 생각이 들었습니다.

Reference

SqueezeNet 논문
AlexNet에 대한 설명
3x3 Filter size의 중요성
NiN(Network in Network)에 대한 설명
SqueezeNet에 대한 레포트